Numerical Methods(1) - Binomial Model

This “Numerical Methods” series will be my notes on different kinds of useful numerical methods that are still frequently used in the industry. Binomial tree model will be the first one to be introduced.

Introduction

To build a basic binomial tree, instead of building an N-period model, just let N=3. So the following’s a 3-period model with a bank account $B_t = e^{rt}$ and a stock $S$ with dynamics. About the notation of this model, the superscript represents the stock price and the subscript $t_n = n\Delta t$ for $n = 0, 1,…,N$.

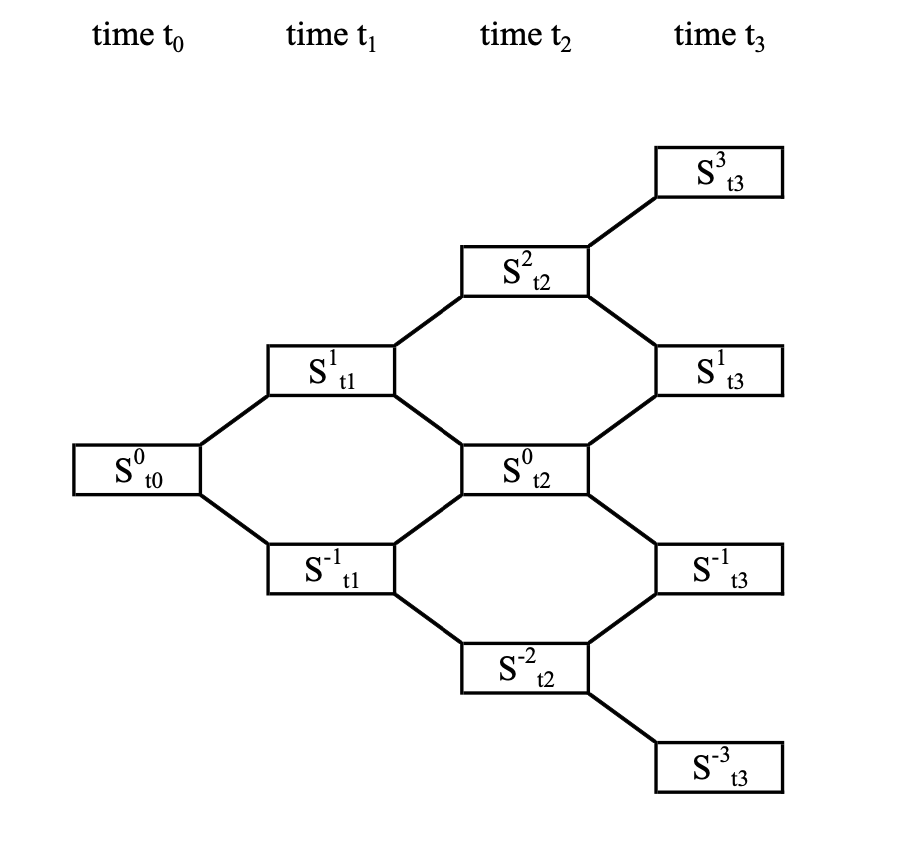
Since we want to use the binomial model to find time-0 price $C_0^{0}$ of some option, based on the model of the stock $S$, we could also build a binomial model for option price $C$ as follows.

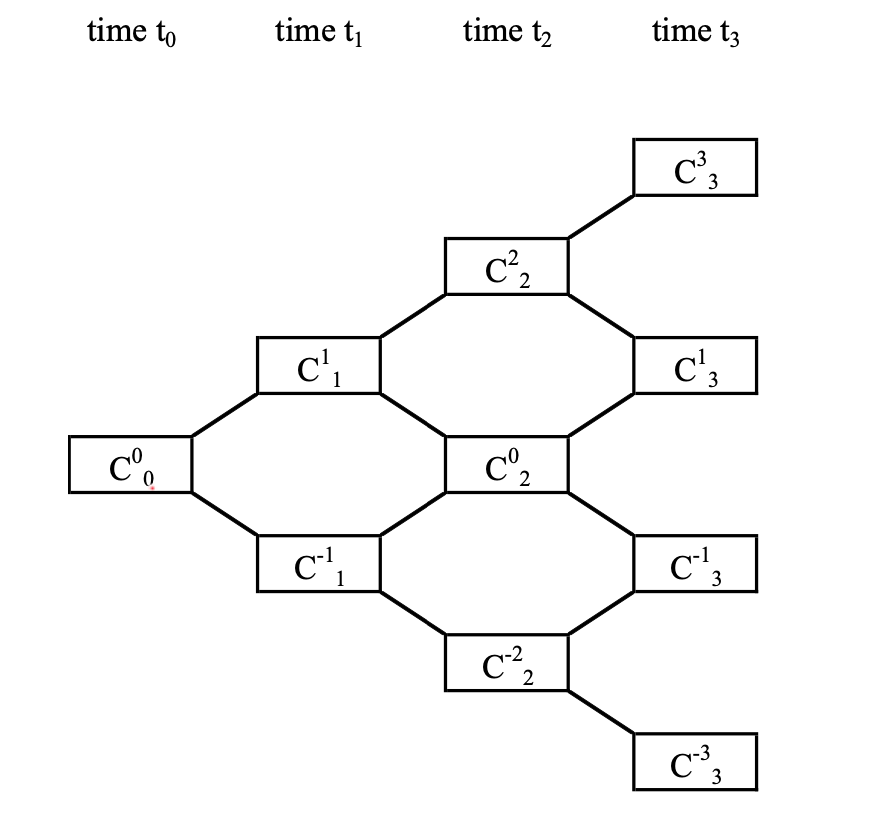
We could use the binomial model to price three kinds of options. They are: European option, up-and-out barrier option and American option.

Pricing an European Option by Binomial Model

If we set $T = t_N$ to be the expiry date of the European option and $f(S)$ to be the payoff function, then for all $j$, the option price is $C_{N}^{j} = f(S_{t_N}^{j})$.

The essence of binomial model is the backward induction. After knowing $C_{n+1}^{j}$, by inducting backwards, we could calculate every node of the binomial tree model. For each ($j, n$), $$ C_{n}^{j} = e^{-r\Delta t}[p_{n}^{j}C_{n+1}^{j+1} + (1 - p_{n}^{j})C_{n+1}^{j-1}] $$ where the up-probability is $$ p_{n}^{j} = \frac{S_{t_n}^{j}e^{r\Delta t} - S_{t_{n+1}}^{j-1}}{S_{t_{n+1}}^{j+1}-S_{t_{n+1}}^{j-1}} $$

Pricing an Up-and-out Barrier Option by Binomial Model

An up-and-out barrier put option on $S$ with strike $K$, expiry $T$ and barrier $H$ pays $$ (K - S_T)^{+} \mathbb{1}{max_{t\in \tau} S_t < H} $$ where $\tau \subseteq [0, T]$ are the ovservation times, specified in the contract. The option price is a functino of three state variables: $$ C(S_{t_n}^{j}, t_n, \mathbb{1}) $$ where the indicator functino is about if the price is knockout prior to time $t_n$ and “knockout prior to time $t_n$” is the event that there exists $t < t_n$ with $t \in \tau$ and $S_t \geq H$. So for the problem, we actuallly only track $C_{n}^{j}:= C(S_{t_n}^{j}, t_n, 0)$.

The payoff function of the up-and-out barrier option $C_{N}^{j} = (K - S_{t_N}^{j})^{+} \mathbb{1}{S_{t_N}^{j} < H \ or \ t_N \notin \tau }$. By inducting backwards, knowing $C_{n+1}^{j}$, for all node ($j, n$) we have two cases: $$ t_n \in \tau \ and \ S_{t_n}^{j}\geq H, $$ in this case, $C_{n}^{j} = 0$, and $$ t_n \notin \tau \ or \ S_{t_n}^{j} < H, $$ in this case, $C_{n}^{j} = e^{-r\Delta t}[p_{n}^{j}C_{n+1}^{j+1} + (1 - p_{n}^{j})C_{n+1}^{j-1}]$.

To sum up, everywhere at or beyond the barrier at monitoring times, set the price to 0; elsewhere, take the usual discounted average of the next-time-step values.

Pricing an American Option by Binomial Model

If we set $T = t_N$ to be the expiry date of the American option and the payoff function, then for all $j$, the option price is $C_{N}^{j} = (K - S_{t_N}^{j})^{+}$. By inducting backwards, since we’ve known $C_{n+1}^{j}$, for each j: $$ C_{n}^{j} = max((K - S_{t_n}^{j})^{+}, e^{-r\Delta t}[p_{n}^{j}C_{n+1}^{j+1} + (1 - p_{n}^{j})C_{n+1}^{j-1}]) $$ To explain, the holder at node ($j, n$) can either excercise and receive $(K - S_{t_n}^{j})^{+}$, or hold on to the option which tomorrow will have no-arbitrage price of $C_{n+1}^{j+1}$(if up) or $C_{n+1}^{j-1}$(if down), which implis:

• if $C_{n}^{j} <$ max, then there’s arbitrage: go long the option.
• if $C_{n}^{j} >$ max, then there’s arbitrage: short the option; if holer exercises, you close out with a profit; if not, then use the funds to buy a portfolio that superreplicates the time-$t_{n+1}$ option value.

The time-0 option price is $C_{0}^{0}$.